Positive, negative and Through-Zero Flanging: probably more than you ever wanted to know about flanging
Don in Portland, OR asks:
"What is the difference between additive and subtractive flanging?"
On the surface, this seems like a quick and easy question, but there's a lot more to flanging than meets the ear. This edition of Straight Jive will be pretty in-depth, so if you're looking for a quick answer here it is:
"Flanging" is the practice of mixing at least two identical signals, with a small delay applied to one or more of the signals. This process creates a complex and incredible, albeit sometimes cheesy sound: the swept comb filter.
As their respective names suggest, additive (positive) flanging simply sums the modulated and static signals, while subtractive (negative) flanging subtracts the modulated signal from the static signal (or vice versa, its all the same). The results of these complimentary operations can be similar, or radically different depending on a few variables detailed below. At the end of the day, it sounds fucking awesome and that's all that really matters. For those of us who have a curious mind, read on...
A brief overview of the process:
Flanging is a pretty bitchin sound. Lets take a look at the basic principals behind the sound before we break down the specific classes of flanging, loosely defined herein as: additive, subtractive and through-zero (both positive and negative, aka: "the ultimate shit").
The first thing we need to do is break down the concept/principal of flanging: a signal (or track) is replicated and a short delay is imparted onto the replicate. This delayed duplicate is then combined with the original and some really cool black-magic-double-voodoo-time-warp-mega-science happens and we get our sound. That's the Reader's Digest version, at least.
The basics:
Imagine in our mix we have a guitar lead line and there's a bend from B to C with a ton of vibrato applied. It just so happens that 1000Hz lies right between B and C. We're gonna hear 1000Hz. Why is 1000Hz significant? Well, its a nice round number, and due to the complexity of this operation, we're gonna wanna keep things as simple as possible. At least for the time being...
So we've got our 1000Hz signal.
We'll use some simple algebraic transformations and a little trig to develop a graphical illustration of that 1000Hz frequency. This will give us a nice picture to look at from all the numbers and theory none-sense:
1000Hz = 1000 cycles per second.
1000 cycles per second = 1S / 1000.
1S / 1000 = 1mS.
1mS = 0.001S.
See where this is going? The illustration below gives us a simplified visual model of our 1000Hz pitch. For this example, the amplitude is 2V peak-to-peak (if these numbers are confusing, you're not alone):
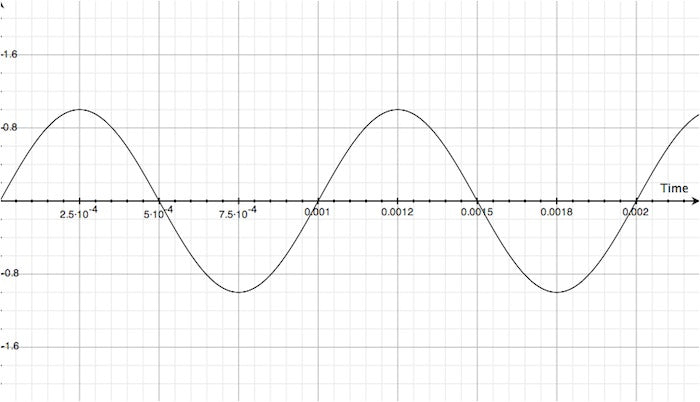

Looks the same, right? Well, it is and it isn't. Remember, that 1000Hz signal has a period of 1mS, so that 1mS delay really just superimposes the second track onto the first! Here's where the differences between Additive and Subtractive flangers begin to present themselves. Introducing:
Additive flanging
The old-school way of doing things. Really, this is the way our ears perceive sound. By adding signals together.
This was probably the first flange sound recorded. Who knows if it was intentional, or a byproduct of too many doobies in the control room. At the end of the day, who gives a rats ass. Without that intent or slip-up we would be missing out on one of the coolest forms of modulation around.
Back to the basics: A track is replicated with a short delay added before it is combined with the original track. In the example above, we're using a 1mS delay on a 1000Hz signal. Check out what happens when the signals are summed:

The smaller wave is our two signals sitting on top of each other before summation, and the big wave is our two signals after summation. That's right, the signal's amplitude doubles! This happens because we are added the same signal to itself, as the signals share the same position in the time domain. Pretty simple and neat, huh?
So that's at 1000Hz. Have a look at what happens to the wave if we vary our delay from 1mS to 2mS. Its pretty wild:
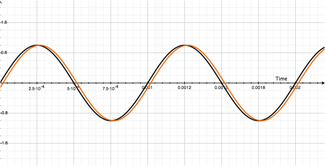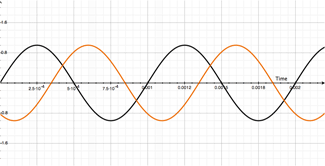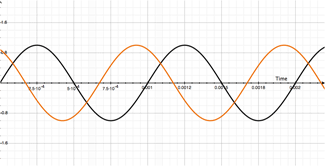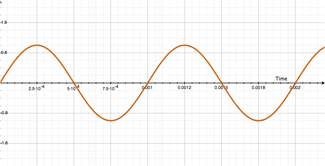
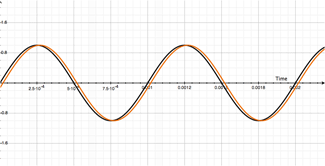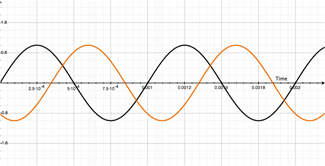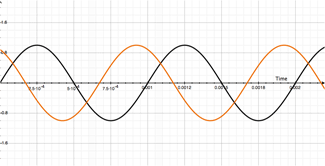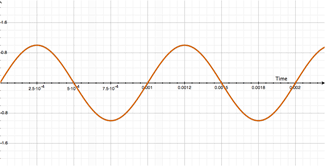
The movie on the left shows our original 1000Hz signal (dry - in black) and with the duplicate-delayed (modulated in orange) signal being delayed from 1mS to 2mS.
The movie on the right shows both our dry (in black), modulated (in orange) and resulting output signal (in purple).
Stop for a second and watch what is happening to our output (purple) signal!
When the modulated signal (orange) is directly over-layed on top of our dry signal, the output signal's amplitude doubles! Regardless of whether the total delay is 1mS, or 2mS. And if you guessed it wouldn't matter if it was 3mS, 4mS, 5mS, etc, you are one smart cookie and you've earned your beers for the day.
If we were to create a simple arithmetic example, we could say that at 1mS delay:
Dry = 1
Modulated = 1
Thus: Dry + Modulated = 1 + 1 = 2
Something interesting happens when the modulated (orange) signal is delayed by 1.5mS. At 1.5mS total delay, it is exactly 180° out of phase with the dry (black) signal. This means they are mirror images of one another. In other words, the same amplitude with the sign reversed. Now our little arithmetic model looks like this:
Dry = 1
Modulated = -1
Thus: Dry + Modulated = 1 + (-1) = 0
Pretty straight forward huh? We made short work of that none-sense real quick. But what about when the delay is at 1.2mS?
Well, not only is our amplitude larger (although not completely doubled) our phase angle (or in this case position in time has changed as well. Pretty interlesting, no? (and yes, that is an intentional typo).
This might not seem like a real big deal, but that's because we are only looking at one single frequency. Dig this. Shit is about to get crazy. Lets look at what happens to the first harmonic of our 1000Hz signal when we add the modulated signal:

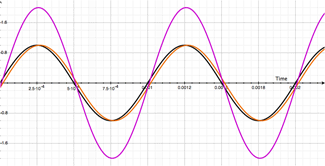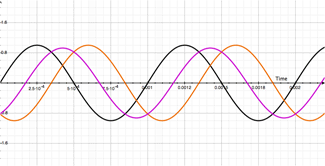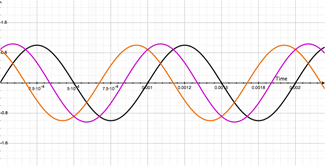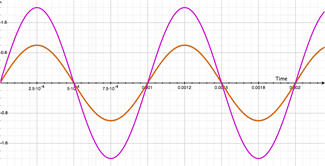
The illustration on the left shows our dry signal (in black) sitting casually alongside our first harmonic (2000Hz shown in green). The squiggly looking blue line is the resulting summation of these two signals. You can see what's happening by combining the green and black lines. When they are both above the center line, the result is positive (as show just past 0 seconds), but things start to get a little wild at just beyond 0.0025 seconds. The green line (our first harmonic) dips below the zero line and becomes negative. When added to our fundamental (dry, shown in black) the result could be positive or negative depending on the values of each lines at the specific instance in time. If you just look at the blue line (the resulting sum of the two) you can begin to see how the two combine together to form a wacky-looking combination of the two, directly related to each signal!
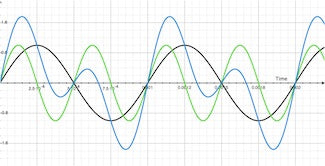
Now to make things really wild: Look at the movie on the right.
The first harmonic is shown in green. The modulated signal is shown in orange and the resulting output of the modulated signal and first harmonic is shown in blue. Pretty crazy, huh? Yeah, it makes my head hurt too.
If you focus on one place in time (vertical line) you will see that the output signal (blue line) relates to the position of both the modulated signal (orange) and first harmonic (green). Its a little tricky and confusing because the orange line is constantly moving, but if you give it a sec, you'll see what's happening. Trust me.
Now to put a fun twist on things, take a step back and look at how the blue line line seems to move in the opposite direction as the orange line. Crazy huh? That little dip that looks like its going backwards actually isn't moving that much. Its centralizing about the lowest point in the first harmonic (dips in the green line) and moving in a circle around it. Similarly with the peaks in the blue line. Dig it. Its really trippy. What's even trippier is the circles created by the moving dips and peaks in the blue line rotate in the opposite direction from one another.
So what do all these colored, squiggly, moving lines mean? Well, its kinda complex because we're only looking at two isolated instances of frequencies which are linearly related to one another, but the basic idea is that we are creating some pretty heavy frequency emphasis and cancellation within the audio band that are all related to one another. The essence of flanging!
Imagine what happens when we look at not only the fundamental and first harmonic, but the frequencies surrounding our fundamental as well as their harmonics. That squiggly line is gonna get even squigglier, and we're gonna end up with a pretty complex and multi-dimentional sound. Yup. In addition to designing pedals, I make up words too.
I hope you've learned something so far, because we're gonna take it up a notch and introduce:
Subtractive flanging
The new-skool way of doing things. Subtractive flanging is a little "stronger" for lack of a better word. Now I don't have proof, and some may call me a bold-faced liar, but I believe subtractive flanging originated in the late 70's, probably in Japan. The rub with flanging had always been that that amazing, orgasmic, nut accomplished on dual tape decks was really expensive and complicated to put into an outboard piece of gear, let alone a foot pedal. Of course, at Mr. Black, we don't think anything of anyone elses' troubles. Shit, we just design the circuit to meet the application. And then you have TunnelWorm TZF. A tiny through-zero flanger with dynamic regeneration and the flexibility to cover through-zero tones, "traditional" flange tones, and even get into chorus territory. Anyone who says it isn't possible... well, I've designed two through-zero flangers now.
So why make a subtractive flanger, Jack? You still haven't answered the initially posed question (that we didn't ask, by the way).
Again, subtractive flanging is "thicker," "stronger," "wetter," "goopier," and a bunch of other suggestive adjectives. In short, its much more pronounced that additive flanging. Perfect for selling a little pedal! Why would anyone buy the pedal that is *kinda* cool, when they could get the wacky, metallic, super flanger by Joe's pedal company? They wouldn't. Thus subtractive flanging was born. At least, that's what I've gathered.
Subtractive flanging is pretty similar to additive flanging. The primary difference is how the signals (dry and modulated) are combined. If you guessed that in an additive flanger, the two signals are merely combined, you should have gone to college. Maybe you did, and that's why you went to college. In a subtractive flanger, the dry and modulated signals have inverse signs when they are combined. That is to say, if the dry signal is positive, the modulated signal is negative (or 180° out of phase with respect to the dry) or vice versa. It might seem like a little thing, but it really changes the characteristic of the sound.
The big reason for this is that when the modulated signal approaches is shortest delay, it is negative with respect to the dry signal. This is beginning to touch on the concept of subtractive Through-Zero Flanging (aka: "the ultimate shit"). Check out the illustrations below and it'll all snap into place:

Here is our dry signal (shown in black) and our modulated signal (shown in orange) at the same ol 1mS delay. Notice anything different about this picture? Yup. The signals are opposite signs. That's because we're subtracting the modulated signal from the dry signal. That means at 1mS, the resulting output will be 0, just like additive flanging's output at 1.5mS. Simple enough, right? Have a look at theses moving pictures and dare to compare! Additive up above, subtractive down below:



You can easily see the difference when the two are sitting directly above and below one another. Essentially the same process is happening, but the phase angle is 180° out. This may seem trivial, but we get a zero output signal at 1mS rather than double the output at 1mS. Why is this significant? Well keep in mind all this is happening at t = 1mS and our output signal (purple) is really the combination of our dry (black) and our modulated signal (orange). Imagine if that 1mS delay was really 0.1mS delay? Or 0.001mS delay? We'd be approaching full cancellation when the cycle was at its peak, as compared to nearly fully doubling the signal. And THIS is why subtractive flanging is more pronounced. Especially if you only use one delay line, which most flangers do.
Now, for the grand finalé. The real deal Holyfield. The big poppa. The mother of all flangers. Where the sound came from, and the moment you've all been waiting for:
Through-Zero Flanging
Through-Zero Flanging is what flanger pedals were trying to replicate. This sound is responsible for flanger pedals existing in the first place. So why are there so few available? Shit, you've read this far. Is this simple shit? Now you're telling me there is more than one modulated delay needed? So we've gotta do all this crap at least twice? AND eliminate the potential for heterodyning? Yup. Its not easy. That's why there aren't a whole bunch of through-zero flangers available.
Lets start by talking about the concept and difficulty in executing the through-zero flange tone. What the hell does through-zero mean anyway? Well, its a slang way of saying the modulated delay matches up to and passes in front of the dry signal. Seems easy enough, right? ehh... kinda... and here's the bitch of the whole thing:
How do you make the modulated signal occur before the dry signal? After all, it hasn't happened yet since the dry signal is happening in real time!? Elementary my dear Watson. A short delay is added to the dry signal, thus creating a slight latency between when signal goes into the circuit and when signal comes out of the dry path. A delay so short, so trivial, so minute it is imperceivable by mere mortals. UNTIL: the modulated delay matches up with it in time at the Zero Point. Oh lord does that make the sound.
You can hear a fine example of that sound on the TunnelWorm TZF page.
Still have questions unanswered? Drop a line, ask away. I probably missed something. It's late and you need a beer.